近日,信息科学与工程学院讲师徐敬可在《IEEE TRANSACTIONS ON COMMUNICATIONS》在线发表了题为“Folded Polynomial Codes for Coded Distributed AA^T-Type Matrix Multiplication”的研究论文。徐敬可老师为该论文的第一作者。
得益于分布式计算平台和分布式计算框架的优良性能,以大规模矩阵乘积为核心的机器学习算法和大数据分析技术得到了快速发展。然而,由于网络延迟、资源共享、系统维护和功率限制等因素,分布式计算系统的工作节点会出现暂时失效等未能完成计算任务的问题,我们称之为称为节点掉队问题。
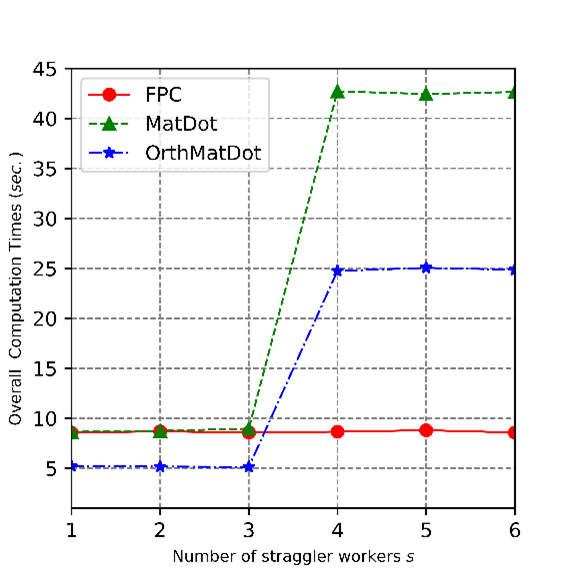
为了缓解节点掉队的影响,针对矩阵与其转置矩阵乘法,本研究利用折叠多项式设计了一类的新颖高效的分布式编码算法。本文的关键技术是利用对称性,将解码问题转化为折叠多项式的重构问题,进而利用无向图的连通性确定了折叠多项式码的恢复阈值。与现有算法相比,在保持原有节点计算复杂度的前提下,折叠多项式码可以忍受更多的掉队节点,有更小的通信代价、更低的译码复杂度等优势。在相同掉队节点的情形下,由于具有抵抗更多掉队节点的优良性能,折叠多项式码可以应用于更经济的分布式计算平台。因此,该研究具有更广泛的应用价值。
该研究得到了国家自然基金项目、国家重点研发计划项目、山东省自然科学基金项目、山东省“青创团队计划”项目、广东省基础与应用基础研究基金项目的资助。
原文链接:DOI: 10.1109/TCOMM.2023.3286420
编 辑:万 千
审 核:贾 波









